C语言程序设计基础PTA考试复习资料

选择判断题

已知字符 B的ASCII码是66，那么也可以通过转义符 \，用 '\66'来表示字符常量 B。（F）

定义变量 int a;，则表达式 a = 3, 5; 执行过后，a的值和表达式的值分别是：（3 , 5）

#include <math.h> 对应的方法是fabs()，而不是abs()

在对数组全部元素赋初值时，不可以省略行数，但能省略列数。（F）

函数strcmp从头至尾顺序地将其对应字符比较，遇到两个字符不等时，两个字符相减得到一个int型值，两个字符串完全相同时，则返回0。（T）

指向数组元素的指针只可指向数组的首元素。（F）

对于已正确定义的二维数组a, *(a[i]+j)与a[i][j]的含义相同。（T）

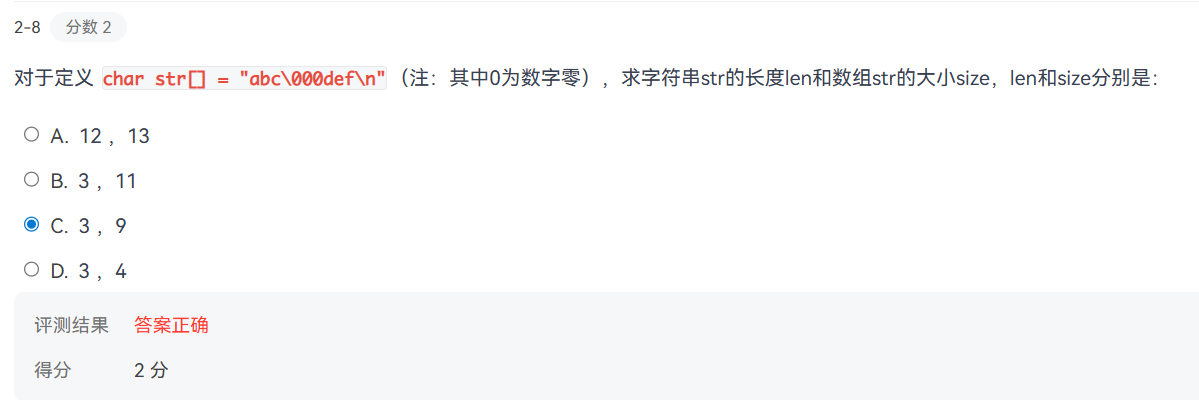
字符串字面值的内部字符序列

"abc\000def\n" 会被编译器解析为以下字符（用 ASCII 码表示）：

'a' → 97
'b' → 98
'c' → 99
'\000' → 八进制转义，值为 0（即空字符 '\0'）
'd' → 100
'e' → 101
'f' → 102
'\n' → 换行符（ASCII 10）
最后还有一个隐含的字符串结束符 '\0'（因为这是双引号字符串字面值）。

字符串长度 len

len 是指用 strlen(str) 计算的结果，即从开头到第一个 '\0' 之前的字符个数。

这里第一个 '\0' 出现在 'c' 之后（第 4 个字节，下标 3），所以：
strlen(str) = 3（字符 'a','b','c'）。

3. 数组大小 size

char str[] 用字符串字面值初始化，数组大小等于整个初始值（包括末尾隐含的 '\0'）的字符数。

我们数一下上面字节序列的总数：

a
b
c
\000
d
e
f
\n
\0（自动添加的结尾）

一共 9 个 char。

所以 sizeof(str) = 9。

程序题

水仙花数判断

问题描述
水仙花数是指一个三位数，其各位数字立方和等于该数本身。例如：153 = 1³ + 5³ + 3³。输入一个三位数，判断是否为水仙花数。
输入格式
一个三位整数。
输出格式
如果是水仙花数，输出 Yes；否则输出 No。

#include <stdio.h>
#include <math.h>

int main(){
    int num;
    scanf("%d",&num);
    if(pow(num/100,3)+pow(num/10%10,3)+pow(num%10,3)==num){
        printf("Yes");
    }else{
        printf("No");
    }
}

统计大小写字母数目

从键盘读入不超过20个字符，统计其中大写字母、小写字母、数字、其他字符的个数。

#include <stdio.h>
#include <string.h>

int main() {
    char str[21];
    int upper = 0, lower = 0, digit = 0, other = 0;
    if (fgets(str, sizeof(str), stdin) != NULL) {
        int len = strlen(str);
        if (len == 20 && str[19] != '\n') {
            printf("ERROR\n");
            return 0;
        }
        for (int i = 0; i < len && str[i] != '\n'; i++) {
            if (str[i] >= 'A' && str[i] <= 'Z') upper++;
            else if (str[i] >= 'a' && str[i] <= 'z') lower++;
            else if (str[i] >= '0' && str[i] <= '9') digit++;
            else other++;
        }
        printf("%d,%d,%d,%d\n", upper, lower, digit, other);
    }
    return 0;
}

十进制转N进制

任务描述

将十进制非负整数M转换成N进制数。（N进制的数有0，1，2，...，N-1共N个数字，逢N进1。）（用循环解决）
其中，1000000>=M>=0，10>=N>=2。

输入格式:

若干行，每行2个整数M和N，代表一组数据。

输出格式:

依次输出每组数据转换成的十进制数，每个输出结果单独占一行。

输入样例:

10 4
100 8
56 7

输出样例:

22
144
110

#include <stdio.h>

int main() {
    int M, N;
    while (scanf("%d %d", &M, &N) != EOF) {
        if (M == 0) {
            printf("0\n");
            continue;
        }
    
        int digits[32]; 
        int len = 0;
    
        int num = M;
        while (num > 0) {
            digits[len++] = num % N;
            num /= N;
        }
    
        for (int i = len - 1; i >= 0; i--) {
            printf("%d", digits[i]);
        }
        printf("\n");
    }
  
    return 0;
}

字符串循环左移

输入一个字符串和一个非负整数N，要求将字符串循环左移N次。

输入格式：

输入在第1行中给出一个不超过100个字符长度的、以回车结束的非空字符串；第2行给出非负整数N。

输出格式：

在一行中输出循环左移N次后的字符串。

输入样例：

Hello World!
2

输出样例：

llo World!He

#include <stdio.h>
#include <string.h>

int main() {
    char str[101];
    int n, len;
  
    fgets(str, 101, stdin);
    len = strlen(str);
    if (str[len - 1] == '\n') {
        str[len - 1] = '\0';
        len--;
    }
  
    scanf("%d", &n);
  
    n = n % len;
  
    for (int i = n; i < len; i++) {
        printf("%c", str[i]);
    }
    for (int i = 0; i < n; i++) {
        printf("%c", str[i]);
    }
  
    return 0;
}