JiomLan's World

large picture of the cover

PyTorch框架深度学习笔记01

PyTorch框架深度学习笔记01(准备篇)

PyTorch，由 Facebook 的人工智能研究团队开发的开源深度学习框架，也是当下几乎最热门的深度学习框架。

PyTorch环境的搭建

Anaconda的安装

如果你有耐心且掌握魔法，那么可以到官网进行下载。

image-kgwd.png

不过官网下载全流程比较繁琐，还要登录，而且速度比较慢。

所以这里我推荐从清华镜像进行下载，国内就可以很快完成下载。

我们在清华镜像的 anaconda/archive/ 下寻找自己需要的版本，这里一定要注意看文件标注的版本和操作系统。在下载好后，我们就可以进行安装了。

image-fobv.png

安装完成后，我们就要配置系统环境变量了，注意一定是系统环境变量。

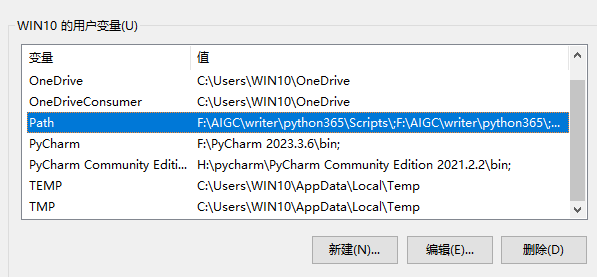
image-fdve.png

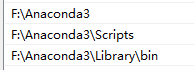
我们在Path里面添加 Anaconda 的安装目录下的三个目录（分别如下）

image-iwkg.png

然后就能在cmd窗口中检查是否配置成功了。

image-vcwm.png

在 Anaconda 安装成功后，我们的电脑上就会多出来一堆相关软件。

image-xpii.png

接下来启动 Anaconda Prompt

image-btzb.png

接下来我们创建一个python环境 conda create -n pytorch python=3.9

这个环境名称是 pytorch，python 版本是3.9。不选择高版本 python 是因为深度学习用不到高版本的 python，且3.9是一个成熟稳定的版本，有很多兼容性很好的第三方库。

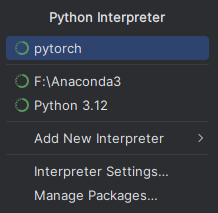
image-vvnf.png

安装完成后，你就能在你的IDE中找到这个环境了。

PyTorch的安装

回到 Anaconda Prompt，输入 conda activate pytorch 进入到我们的环境中，然后输入 nvidia-smi 查看CUDA版本。

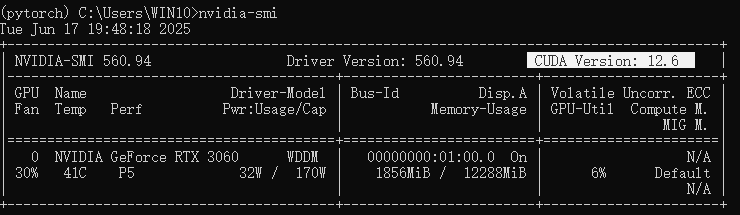
image-hecs.png

这里我的 CUDA 版本是12.6，接下来就要去 PyTorch 官网 进行安装了。

image-dxes.png

注意，一定要按照自己的 CUDA 版本和 Python 版本选择安装。

pip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu126

然后继续在刚才的终端输入安装命令即可，如果是在清华镜像安装的 Anaconda ，这一步安装时候会自动安装清华镜像内的 PyTorch ，因此不需要科学上网。

深度学习的一般步骤

深度学习 = 表示学习 + 浅层学习

原始数据——>[(底层特征——>中层特征——>高层特征)——>预测]——>结果

对于机器学习来说，数据集和数据集的预处理是非常重要的一个环节，甚至某些情况下可以起到决定性的作用，因此对数据集进行预处理是必要的步骤。

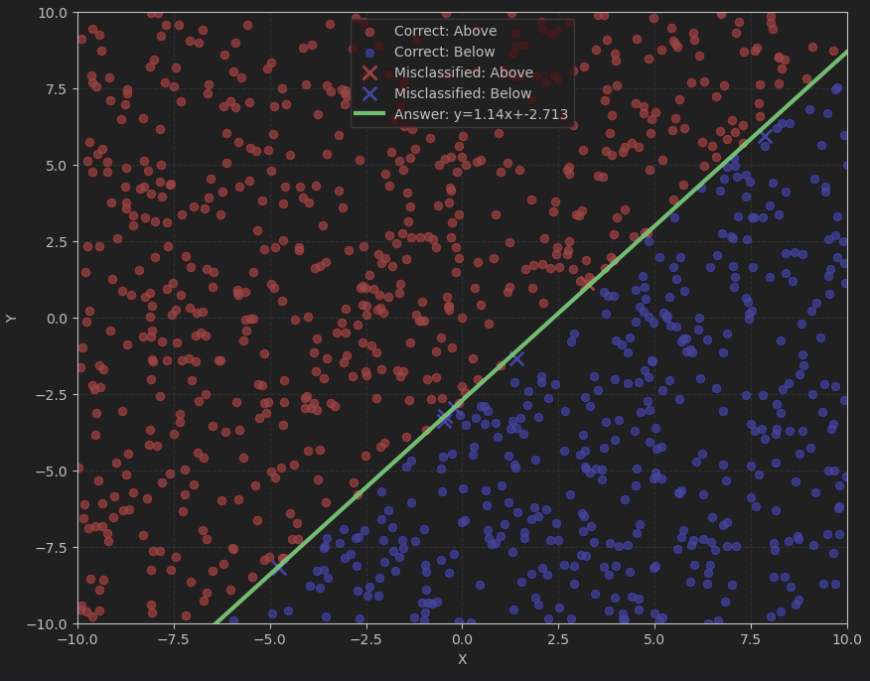
本次对PyTorch框架的学习主要在图像分类方面，因此，图像数据集的重要性不必多谈，而接下来相对重要的步骤在于图像分类的方法设计。我计划将按照KNN、CNN的顺序进行PyTorch框架下的学习，不过也会先通过SVM等二分类分类机进行练手。

既然是学习，自然要多学到点知识才好，所以我会尽量尝试各种损失函数、正则化，观察不同训练后的结果，这样或许有助于更好的理解现在深度学习解决欠拟合和过拟合的技术，并且也可以自己尝试设计函数来观察不同的结果。

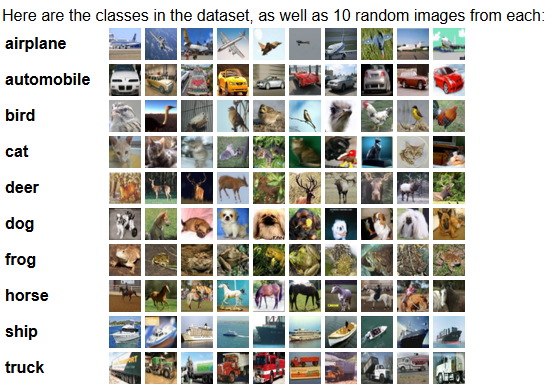
计算机视觉数据集

·MNIST手写数字训练集

·CIFAR数据集

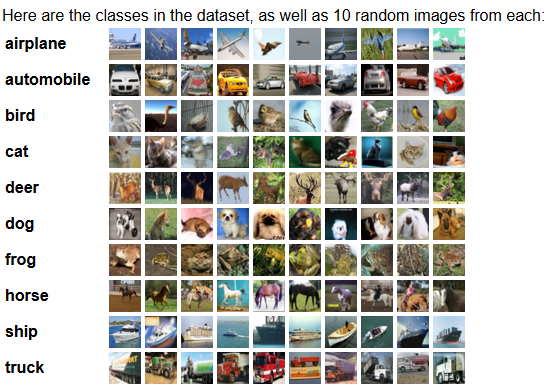
image-iazp.png

未来会用到的Python库

NumPy

强大的数据处理库，也可以结合SciPy进行使用

import numpy as np
print(np.__version__) #版本输出

#用array()导入向量与矩阵
vector = np.array([1,2,3,4])
# type(vector) ——> <class 'numpy.ndarray'>
# ndarray:N Dimensions Array
matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])

NumPy

菜鸟教程

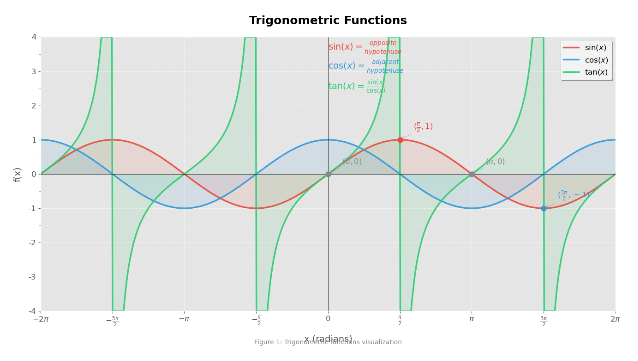
Matplotlib

图像绘制库，实现数据可视化。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator

# 设置全局样式
plt.style.use('ggplot')

# 创建图形和坐标轴
fig, ax = plt.subplots(figsize=(14, 8), dpi=100)

# 生成数据点
x = np.linspace(-2*np.pi, 2*np.pi, 1000)
sin_y = np.sin(x)
cos_y = np.cos(x)
tan_y = np.tan(x)

# 避免正切函数的不连续点
tan_y = np.clip(tan_y, -4, 4)  # 限制y值在[-4, 4]范围内

# 绘制三角函数曲线
sin_line, = ax.plot(x, sin_y, color='#E74C3C', linewidth=2.5, alpha=0.9,
                   label=r'$\sin(x)$', marker='', linestyle='-')
cos_line, = ax.plot(x, cos_y, color='#3498DB', linewidth=2.5, alpha=0.9,
                   label=r'$\cos(x)$', marker='', linestyle='-')
tan_line, = ax.plot(x, tan_y, color='#2ECC71', linewidth=2.5, alpha=0.9,
                   label=r'$\tan(x)$', marker='', linestyle='-')

# 添加渐变色填充
ax.fill_between(x, sin_y, 0, color='#E74C3C', alpha=0.1)
ax.fill_between(x, cos_y, 0, color='#3498DB', alpha=0.1)
ax.fill_between(x, tan_y, 0, color='#2ECC71', alpha=0.1)

# 设置标题和标签
ax.set_title('Trigonometric Functions', fontsize=18, fontweight='bold', pad=20)
ax.set_xlabel('x (radians)', fontsize=14, labelpad=10)
ax.set_ylabel('f(x)', fontsize=14, labelpad=10)

# 设置x轴刻度（以π为单位）
ax.set_xticks([-2*np.pi, -3*np.pi/2, -np.pi, -np.pi/2, 0,
               np.pi/2, np.pi, 3*np.pi/2, 2*np.pi])
ax.set_xticklabels([r'$-2\pi$', r'$-\frac{3\pi}{2}$', r'$-\pi$',
                   r'$-\frac{\pi}{2}$', '0',
                   r'$\frac{\pi}{2}$', r'$\pi$',
                   r'$\frac{3\pi}{2}$', r'$2\pi$'], fontsize=12)

# 设置y轴刻度和网格
ax.set_yticks([-4, -3, -2, -1, 0, 1, 2, 3, 4])
ax.set_yticklabels([-4, -3, -2, -1, 0, 1, 2, 3, 4], fontsize=12)
ax.yaxis.set_minor_locator(MultipleLocator(0.5))

# 添加网格线
ax.grid(True, linestyle='--', alpha=0.7, which='both')
ax.grid(True, linestyle=':', alpha=0.4, which='minor')

# 添加零线
ax.axhline(0, color='black', linewidth=0.8, alpha=0.7)
ax.axvline(0, color='black', linewidth=0.8, alpha=0.7)

# 设置坐标轴范围
ax.set_xlim(-2*np.pi, 2*np.pi)
ax.set_ylim(-4, 4)

# 添加图例
legend = ax.legend(loc='upper right', frameon=True, shadow=True,
                  fontsize=12, framealpha=0.95)
legend.get_frame().set_facecolor('#F8F9F9')

# 添加关键点的注释
key_points = [
    (0, 0, r'$(0, 0)$', '#7F8C8D'),
    (np.pi/2, 1, r'$(\frac{\pi}{2}, 1)$', '#E74C3C'),
    (np.pi, 0, r'$(\pi, 0)$', '#7F8C8D'),
    (3*np.pi/2, -1, r'$(\frac{3\pi}{2}, -1)$', '#3498DB')
]

for x_val, y_val, text, color in key_points:
    ax.plot(x_val, y_val, 'o', markersize=8, color=color)
    ax.annotate(text, (x_val, y_val),
                xytext=(x_val + 0.3, y_val + 0.3),
                fontsize=12, color=color,
                arrowprops=dict(arrowstyle='->', color=color, alpha=0.7))

# 添加数学公式注释
ax.text(0.5, 0.95, r'$\sin(x) = \frac{opposite}{hypotenuse}$',
        transform=ax.transAxes, fontsize=14, color='#E74C3C')
ax.text(0.5, 0.88, r'$\cos(x) = \frac{adjacent}{hypotenuse}$',
        transform=ax.transAxes, fontsize=14, color='#3498DB')
ax.text(0.5, 0.81, r'$\tan(x) = \frac{\sin(x)}{\cos(x)}$',
        transform=ax.transAxes, fontsize=14, color='#2ECC71')

# 添加图表说明
ax.text(0.5, -0.12, 'Figure 1: Trigonometric functions visualization',
        transform=ax.transAxes, fontsize=10, ha='center', color='#7F8C8D')

# 添加边距使图形更美观
plt.tight_layout(pad=3.0)

# 显示图形
plt.show()

image-bjss.png

基础的PyTorch语法

完整代码点这里

导入PyTorch库

import torch

检查是否启用GPU

print(torch.cuda.is_available())

创建和处理张量(Tensor)

a = torch.rand(2,3)
b = torch.rand(2,3)
#创建一个两行三列的随机张量，填充随机数
#Returns a tensor filled with random numbers from a uniform distribution on the interval [0,1)
print(a)
print(b)
#计算张量a中所有数据的和，用type函数得到数据类型，可知返回值仍然是一个张量
print(type(a.sum()),a.sum())
#访问a张量第二行第二列的元素
print(type(a[1,1]),a[1,1])
#a张量与b张量相乘
print(type(a*b),a*b)
#获取张量a中的最大值
print(a.max())
#数据处理
print(a[0,0]<1)
print(a[0,0]+1)

其余代码已经上传到Github上，点击蓝色链接即可在Github中预览ipynb程序，并且可以预览输出结果（Jupyter的优越性）

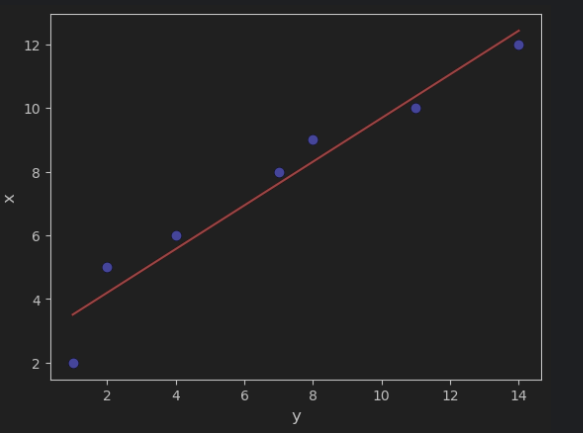
练习：通过最小二乘法实现线性回归

线性回归（Linear Regression）是机器学习中最基础的算法之一，这是一种用来预测连续数据的算法，它建设目标变量 y 和特征变量 x 之间存在线性关系，并且来找到一条最佳拟合直线来描述这种关系。

import numpy as np
import matplotlib.pyplot as plt

因为不用训练，所以这里只用到了Numpy库进行数据处理。

接下来，我们通过最小二乘法进行线性回归。

a = \frac{\sum_{i=1}^{n}\left ( x_{i}-\bar{x} \right )\left ( y_{i}-\bar{y} \right ) }{ \sum_{i=1}^{n}\left ( x_{i}-\bar{x} \right )^{2} }
b = \bar{y} -a\bar{x}
x = np.array([1, 2, 4, 7, 8, 11, 14]) 
y = np.array([2, 5, 6, 8, 9, 10, 12])  
x_mean = np.mean(x)
y_mean = np.mean(y)
a=0
b=0
denominator = 0.0       # 分母
numerator   = 0.0       # 分子

#利用高中学过的最小二乘法进行线性回归
for _x,_y in zip(x,y):
    numerator +=(_x-x_mean)*(_y-y_mean)  
    denominator += (_x-x_mean)**2
a = numerator/denominator
b = y_mean - a * x_mean

#得到线性回归方程 y = ax + b
y_predict = a*x + b

plt.scatter(x, y, color='b', marker='o')
plt.plot(x, y_predict, color='red')
plt.xlabel('y', fontsize=12)
plt.ylabel('x', fontsize=12)
plt.show()

image-gcww.png

为梦想创造现实！

site logo

Hi,Dreamweaver

© 2025 JiomLan's World